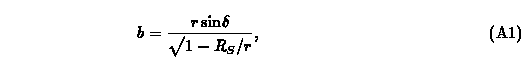
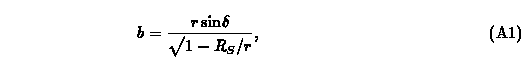
where delta is the angle the photon's velocity makes with the radial direction. For a lens large enough not to exhibit a photon sphere (R_* > 1.5 R_S), the limb of the source will be seen when a photon leaving the source tangentially grazing its surface, such that r = R_* and delta = pi/2. Then
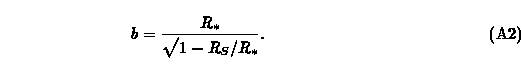
This photon will reach the observer with $r = D$ and angle to the center of the lens of delta_obs such that
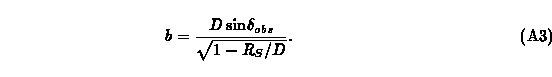
Equating Eqs. (A2) and (A3) and solving for delta_obs yields
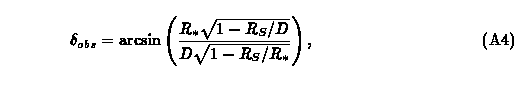
which is the apparent size of the lens.
When the lens is compact enough to be surrounded by a photon sphere, one can simply replace R_* in the above expression with 1.5 R_S, as these photons now define the apparent size of the lens. The result is
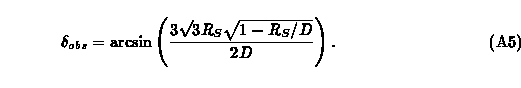
Be careful to assign the correct quadrant to the result. If R_* < 1.5 R_S, then delta_obs will be greater than pi/2.