INTRODUCTION



Next: DISTANCE DETERMINATION IN
Up: HOW FAR AWAY ARE
Previous: HOW FAR AWAY ARE
The information about the observed properties of gamma-ray
bursts was provided by Dr. Fishman
in his introductory paper. I shall summarize what
I consider to be the most important for their distance scale.
The observed distribution of gamma-ray bursts appears to be isotropic.
It is true that a number of researchers found small departures from
perfectly uniform distribution by selecting various
sub-samples of the bursts (e.g. Lamb & Quashnock 1994), but these small
irregularities were not confirmed by the new data,
and even the correctness of the original claim is in
doubt (Rutledge & Lewin 1993). It is natural that
any finite sample must exhibit some statistical fluctuations, giving
evidence for things which are not, in fact, there. So far no
specific suggestion of anisotropy survived the test of time. To the
contrary, the more bursts are known the more isotropic their distribution
appears, as the statistical fluctuations average out.
There was a lot of confusion in the 1980s about
the correct way of measuring burst intensity. By ``correct'' I mean the
way which would be proper to study their radial distribution.
After some debate a consensus has been reached: the burst intensity has to
be measured in the same units which are used to detect the bursts.
Roughly speaking it is the number of photons detected in a time bin
of a chosen duration. For example, if a burst is detected when the
count of photons in one second intervals exceeds some threshold,
then the peak count per second should be used as a measure of the
burst intensity.
It is well known that if
sources of any kind are uniformly distributed in a 3-dimensional Euclidean
space then the number of sources, 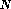 , that appear to be brighter
than some limit
, that appear to be brighter
than some limit 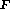 is proportional to that limit in power -1.5, that is
we have:
is proportional to that limit in power -1.5, that is
we have: 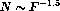 . The reason is simple: the sources that appear
a factor
. The reason is simple: the sources that appear
a factor 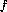 brighter are a factor
brighter are a factor 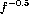 farther away, and therefore
they are detectable in a volume that is a factor
farther away, and therefore
they are detectable in a volume that is a factor 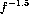 larger, and
hence they are more numerous by a factor
larger, and
hence they are more numerous by a factor 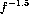 . For this relation
to hold, the statistical properties of distant
sources should be the same as the statistical properties
of nearby sources, and the average number of sources per unit
volume should be constant. This relation is observed to be approximately
satisfied by the bright stars as well as by the bright galaxies, even
though the nature of the two types of objects, as well as their distances,
are very different.
. For this relation
to hold, the statistical properties of distant
sources should be the same as the statistical properties
of nearby sources, and the average number of sources per unit
volume should be constant. This relation is observed to be approximately
satisfied by the bright stars as well as by the bright galaxies, even
though the nature of the two types of objects, as well as their distances,
are very different.
The best statistics of bright gamma-ray bursts is provided by the instrument
PVO - Pioneer Venus Orbiter, which was collecting information for 13 years,
and registered over 200 strong bursts
(Fenimore et al. 1992). The distribution of these bursts
is well approximated with the relation 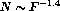 , indicating that
the sources of apparently strong, and presumably relatively nearby bursts,
have a uniform number density out to some distance.
The most sensitive instrument to date is BATSE, roughly 30 times more
sensitive than PVO.
The distribution of BATSE bursts may be approximated with the relation
, indicating that
the sources of apparently strong, and presumably relatively nearby bursts,
have a uniform number density out to some distance.
The most sensitive instrument to date is BATSE, roughly 30 times more
sensitive than PVO.
The distribution of BATSE bursts may be approximated with the relation
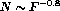 (Meegan 1992), indicating that the number of apparently weak, and
presumably distant bursts is relatively small, as if there were fewer of
them at large distances, or if the space at some large distance was no longer
Euclidean. The results from instruments with the sensitivity intermediate
between PVO and BATSE is intermediate (Tamblyn & Melia 1993). In fact, when
the PVO and BATSE bursts are combined, a gradual transition from a slope
close to -1.5 on the bright end to -0.8 at the faint end becomes apparent
(Fenimore et al. 1993). It appears that the results from all instruments
provide a consistent view: the relatively nearby bursts are approximately
uniformly distributed with distance, but beyond some distance the number
density of bursters decreases, or the space becomes non-Euclidean.
(Meegan 1992), indicating that the number of apparently weak, and
presumably distant bursts is relatively small, as if there were fewer of
them at large distances, or if the space at some large distance was no longer
Euclidean. The results from instruments with the sensitivity intermediate
between PVO and BATSE is intermediate (Tamblyn & Melia 1993). In fact, when
the PVO and BATSE bursts are combined, a gradual transition from a slope
close to -1.5 on the bright end to -0.8 at the faint end becomes apparent
(Fenimore et al. 1993). It appears that the results from all instruments
provide a consistent view: the relatively nearby bursts are approximately
uniformly distributed with distance, but beyond some distance the number
density of bursters decreases, or the space becomes non-Euclidean.
It is very important to consider the two results together: the isotropic
distribution
in the sky with the apparent shortage of weak bursts in all directions.
The conclusion is: we appear to be at the center, or near the center
of a spherically symmetric and bounded distribution of gamma-ray bursters.
Another very important feature of a gamma-ray burst is its spectrum.
The spectra are very broad, covering many decades of photon energies,
extending in extreme cases to photons as soft as 1 keV, and in some cases
to photons as hard as 18 GeV (Hurley et al. 1994). A typical spectrum may
be approximated with a broken power law (Schaefer et al. 1992, 1994),
and it is so broad that there is no doubt it is non-thermal. I think
there is a consensus on this issue.
It is important to note that while it is
relatively easy to make a model of a nearly thermal stellar spectrum,
regardless of whether the star is radiating mostly in the infrared (like
M-type giants and dwarfs), in the optical (as our sun), in the ultraviolet
(as O-type stars), or even in the X-rays (as X-ray bursts). A thermal
model is uniquely described with its temperature,
and a few other well defined parameters. The situation is very different
for any class of astronomical objects which have clearly non-thermal
spectra, like quasars, radio pulsars, or gamma-ray bursts.
There is no unique way to model such a spectrum and there is no consensus
among the researchers which of the many models of any of the non-thermal
sources is correct.
Invariably, the models invoke free parameters and a lot of more or less
ad hoc assumptions. While the quantitative models of thermal or nearly
thermal sources may even be useful in estimating their distances, nothing
of this sort is possible for any of the sources which have non-thermal
spectra - the diversity of non-thermal models is limited only by the
imagination of theoreticians who study them. I know of no example
of a model of a non-thermal source to be successfully used to deduce
its distance. Therefore, my conclusion is that currently
there is no known way to use the observed spectra to deduce the distance
to gamma-ray bursts.
But not everything is lost. Sometimes a spectrum can be used to deduce
the distance even if we have no idea how the spectrum was formed: we
just use the source as a light bulb, and the fact that it can be seen
may be used for the distance estimate. The
trick is that the matter between the source and the observer may absorb
photons of some energy. For example, interstellar gas is very opaque
to the ultraviolet and soft X-rays
(cf. Paczynski 1991), while TeV photons cannot travel very far through the
intergalactic radiation field (cf. Stecker et al. 1992).
If the spectrum of a source located near the plane of
our galaxy is found to extend into sub-keV domain than the source must
be closer than about 1 kiloparsec from us (well within our galaxy),
as otherwise the interstellar gas
would prevent the soft photons from reaching us. If the spectrum is seen
to extend above 1 TeV then the source cannot be at a distance larger than
about 500 Megaparsecs as the intergalactic infrared radiation
prevents super TeV photons from reaching us from a larger distance.
It is possible that in the future such effects may help us to
estimate the distances to gamma-ray bursters.
The bursts show a tremendous variety of intensity variation, the time
structure and duration (cf. Fishman et al. 1994). In the past, the rapid
time variability was thought to provide some limit on the distance to the
sources. This is no longer so. It is well established that if the source
expands ultra
relativistically then the observed variability is compatible with any
distance (Zdziarski et al. 1991). And there are at least two
reasons to expect ultra-relativistic expansion of gamma-ray bursters
located either in the galactic corona or at cosmological distances.
First, at either distance scale,
the luminosities are highly super-Eddington with the powerful radiation
pressure driving relativistic expansion. Second, the observed spectra
show no cut-off at the pair creation limit, implying the gamma-ray
photons are streaming nearly radially from the ``photosphere'' out.
This is equivalent to an ultra-relativistic flow.
It is my conclusion that at this time we have only one robust distance
indicator for gamma-ray bursters: the apparently isotropic
distribution of bursts in the sky combined with the evidence that
the radial distribution is bounded at the same distance in all
directions.
Following Hakkila et al. (1994) I shall use the term `galactic corona'
rather than 'galactic halo' for one of the currently popular distributions
of gamma-ray bursters. The reason is that the required distribution is
unlike any observed or theoretically proposed galactic halo. According
to the most popular ideas of the galactic origin of the bursters they are
related to the very high velocity neutron stars, which are claimed to
have this novel type of distribution.
It is interesting to note that the two most popular distance
scales are both extragalactic. The nearest galaxies, the Large and
Small Magellanic Clouds, are at the distance of 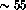 kiloparsecs.
A few other galaxies are at about
kiloparsecs.
A few other galaxies are at about 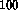 kiloparsec. A typical coronal
gamma-ray burst is believed to be at
kiloparsec. A typical coronal
gamma-ray burst is believed to be at 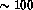 kiloparsecs, i.e. well
into the intergalactic space. Of course, in the cosmological hypothesis
the bursters are even farther away. The only justification to call
the coronal distribution galactic rather than extragalactic is the
origin of the bursters: in the coronal scenario they are thought to be
ejected from our galaxy.
kiloparsecs, i.e. well
into the intergalactic space. Of course, in the cosmological hypothesis
the bursters are even farther away. The only justification to call
the coronal distribution galactic rather than extragalactic is the
origin of the bursters: in the coronal scenario they are thought to be
ejected from our galaxy.



Next: DISTANCE DETERMINATION IN
Up: HOW FAR AWAY ARE
Previous: HOW FAR AWAY ARE
Jerry Bonnell
Tue Jun 6 14:33:23 EDT 1995
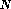 , that appear to be brighter
than some limit
, that appear to be brighter
than some limit 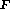 is proportional to that limit in power -1.5, that is
we have:
is proportional to that limit in power -1.5, that is
we have: 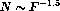 . The reason is simple: the sources that appear
a factor
. The reason is simple: the sources that appear
a factor 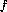 brighter are a factor
brighter are a factor 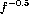 farther away, and therefore
they are detectable in a volume that is a factor
farther away, and therefore
they are detectable in a volume that is a factor 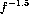 larger, and
hence they are more numerous by a factor
larger, and
hence they are more numerous by a factor 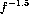 . For this relation
to hold, the statistical properties of distant
sources should be the same as the statistical properties
of nearby sources, and the average number of sources per unit
volume should be constant. This relation is observed to be approximately
satisfied by the bright stars as well as by the bright galaxies, even
though the nature of the two types of objects, as well as their distances,
are very different.
. For this relation
to hold, the statistical properties of distant
sources should be the same as the statistical properties
of nearby sources, and the average number of sources per unit
volume should be constant. This relation is observed to be approximately
satisfied by the bright stars as well as by the bright galaxies, even
though the nature of the two types of objects, as well as their distances,
are very different.
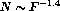 , indicating that
the sources of apparently strong, and presumably relatively nearby bursts,
have a uniform number density out to some distance.
The most sensitive instrument to date is BATSE, roughly 30 times more
sensitive than PVO.
The distribution of BATSE bursts may be approximated with the relation
, indicating that
the sources of apparently strong, and presumably relatively nearby bursts,
have a uniform number density out to some distance.
The most sensitive instrument to date is BATSE, roughly 30 times more
sensitive than PVO.
The distribution of BATSE bursts may be approximated with the relation
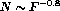 (Meegan 1992), indicating that the number of apparently weak, and
presumably distant bursts is relatively small, as if there were fewer of
them at large distances, or if the space at some large distance was no longer
Euclidean. The results from instruments with the sensitivity intermediate
between PVO and BATSE is intermediate (Tamblyn & Melia 1993). In fact, when
the PVO and BATSE bursts are combined, a gradual transition from a slope
close to -1.5 on the bright end to -0.8 at the faint end becomes apparent
(Fenimore et al. 1993). It appears that the results from all instruments
provide a consistent view: the relatively nearby bursts are approximately
uniformly distributed with distance, but beyond some distance the number
density of bursters decreases, or the space becomes non-Euclidean.
(Meegan 1992), indicating that the number of apparently weak, and
presumably distant bursts is relatively small, as if there were fewer of
them at large distances, or if the space at some large distance was no longer
Euclidean. The results from instruments with the sensitivity intermediate
between PVO and BATSE is intermediate (Tamblyn & Melia 1993). In fact, when
the PVO and BATSE bursts are combined, a gradual transition from a slope
close to -1.5 on the bright end to -0.8 at the faint end becomes apparent
(Fenimore et al. 1993). It appears that the results from all instruments
provide a consistent view: the relatively nearby bursts are approximately
uniformly distributed with distance, but beyond some distance the number
density of bursters decreases, or the space becomes non-Euclidean.
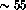 kiloparsecs.
A few other galaxies are at about
kiloparsecs.
A few other galaxies are at about 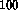 kiloparsec. A typical coronal
gamma-ray burst is believed to be at
kiloparsec. A typical coronal
gamma-ray burst is believed to be at 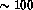 kiloparsecs, i.e. well
into the intergalactic space. Of course, in the cosmological hypothesis
the bursters are even farther away. The only justification to call
the coronal distribution galactic rather than extragalactic is the
origin of the bursters: in the coronal scenario they are thought to be
ejected from our galaxy.
kiloparsecs, i.e. well
into the intergalactic space. Of course, in the cosmological hypothesis
the bursters are even farther away. The only justification to call
the coronal distribution galactic rather than extragalactic is the
origin of the bursters: in the coronal scenario they are thought to be
ejected from our galaxy.