A RELATION BETWEEN DISTANCE AND RADIAL VELOCITY
AMONG EXTRA-GALACTIC NEBULAE
By Edwin Hubble
Mount Wilson Observatory, Carnegie Institution of Washington
Communicated January 17, 1929
Distances of extra-galactic nebulae depend ultimately upon the application of absolute-luminosity criteria to involved stars whose types can be recognized. These include, among others, Cepheid variables, novae, and blue stars involved in emission nebulosity. Numerical values depend upon the zero point of the period-luminosity relation among Cepheids, the other criteria merely check the order of the distances. This method is restricted to the few nebulae which are well resolved by existing instruments. A study of these nebulae, together with those in which any stars at all can be recognized, indicates the probability of an approximately uniform upper limit to the absolute luminosity of stars, in the late-type spirals and irregular nebulae at least, of the order of (photographic) = -6.3.[1] The apparent luminosities of the brightest stars in such nebulae are thus criteria which, although rough and to be applied with caution, furnish reasonable estimates of the distances of all extra-galactic systems in which even a few stars can be detected.
TABLE 1
NEBULAE WHOSE DISTANCES HAVE BEEN ESTIMATED FROM STARS
INVOLVED OR FROM MEAN LUMINOSITIES IN A CLUSTER
object ms r v mt Mt
S. Mag. .. 0.032 + 170 1.5 -16.0
L. Mag. .. 0.034 + 290 0.5 17.2
N.G.C.6822 .. 0.214 - 130 9.0 12.7
598 .. 0.263 - 70 7.0 15.1
221 .. 0.275 - 185 8.8 13.4
224 .. 0.275 - 220 5.0 17.2
5457 17.0 0.45 + 200 9.9 13.3
4736 17.3 0.5 + 290 8.4 15.1
5194 17.3 0.5 + 270 7.4 16.1
4449 17.8 0.63 + 200 9.5 14.5
4214 18.3 0.8 + 300 11.3 13.2
3031 18.5 0.9 - 30 8.3 16.4
3627 18.5 0.9 + 650 9.1 15.7
4826 18.5 0.9 + 150 9.0 15.7
5236 18.5 0.9 + 500 10.4 14.4
1068 18.7 1.0 + 920 9.1 15.9
5055 19.0 1.1 + 450 9.6 15.6
7331 19.0 1.1 + 500 10.4 14.8
4258 19.5 1.4 + 500 8.7 17.0
4151 20.0 1.7 + 960 12.0 14.2
4382 .. 2.0 + 500 10.0 16.5
4472 .. 2.0 + 850 8.8 17.7
4486 .. 2.0 + 800 9.7 16.8
4649 .. 2.0 +1090 9.5 17.0
------
Mean -15.5
ms = photographic magnitude of brightest stars involved
r = distance in units of 106 parsecs.
The first two are Shapley's values.
v = measured velocities in km./sec.
N. G. C. 6822, 221, 224 and 5457 are recent determinations
by Humason.
mt = Holetschek's visual magnitude as corrected by Hopmann.
The first three objects were not measured by Holetschek,
and the values of mt represent estimates by the author
based upon such data as are available.
Mt = total visual absolute magnitude computed from mt and r.
Finally, the nebulae themselves appear to be of a definite order of
absolute luminosity, exhibiting a range of four or five magnitudes
about an average value M (visual) = - 15.2.[1] The application of
this statistical average to individual cases can rarely be used to
advantage, but where considerable numbers are involved, and especially
in the various clusters of nebulae, mean apparent luminosities of the
nebulae themselves offer reliable estimates of the mean distances.
Radial velocities of 46 extra-galactic nebulae are now available, but individual distances are estimated by only 24. For one other, N. G. C. 3521, an estimate could probably be made, but no photographs are available at Mount Wilson. The data are given in table 1. The first seven distances are the most reliable, depending, except for M 32 athe companion of M 31, upon extensive investigations of many stars involved. The next thirteen distances, depending upon the criterion of a uniform upper limit of stellar luminosity, are subject to considerable probable errors but are believed to be the most reasonable values at present available. The last four objects appear to be in the Virgo Cluster. The distance assigned to the cluster, 2 x 10[6] parsecs, is derived from the distribution of nebular luminosities, together with luminosities of stars in some of the later-type spirals, and differs somewhat from the Harvard estimate of ten million light years.[2]
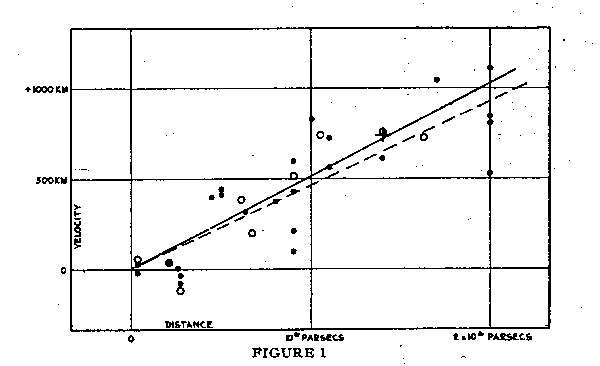
The data in the table indicate a linear correlation between distances and velocities, whether the latter are used directly or corrected for solar motion, according to the older solutions. This suggests a new solution for the solar motion in which the distances are introduced as coefficients of the K term, i. e., the velocities are assumed to vary directly with the distances, and hense K represents the velocity at unit distance due to this effect. The equations of condition then take the form
rK + Xcos(alpha)cos(delta) + Y sin(alpha)cos(delta)+ Zsin(delta) = v.
Two solutions have been made, one using the 24 nebulae individually, the other combining them into 9 groups according to proximity in direction and in distance. The results are
24 objects 9 groups
X - 65 +/- 50 +3 +/- 70
Y +226 +/- 95 +230 +/-120
Z -195 +/- 40 -133 +/- 70
K +465 +/- 50 +513 +/- 60 km./sec. per 10[6] parsecs.
A 286deg. 269deg.
D +40deg. +33deg.
Vo 306 km./sec. 247 km./sec.
For such scanty material, so poorly distributed, the results are fairly definite. Differences between the two solutions are due largely to the four Virgo nebulae, which, being the most distant objects and all sharing the peculiar motion of the cluster, unduly influence the value of K and hence of Vo. New data on more distant objects will be required to reduce the effect of such peculiar motion. Meanwhile round numbers, intermediate between the two solutions, will represent the probably order of the values. For instance, let A = 277deg. , D = +36deg. (Gal. long. = 32deg. , lat. = +18deg. ), Vo = 280 km./sec., K = +500 km./sec. per million parsecs. Mr. Stromberg has very kindly checked the general order of these values by independent solutions for different groupings of the data.
A constant term, introduced into the equations, was found to be small and negative. This seems to dispose of the necessity for the old constant K term. Solutions of this sort have been published by Lundmark,[3] who replaced the old K by k + lr + mr[2]. His favored solution gave k = 513, as against the former value of the order of 700, and hence offered little advantage.
TABLE 2
NEBULAE WHOSE DISTANCES ARE ESTIMATED FROM RADIAL VELOCITIES
object v vs r mt Mt
N.G.C.278 + 650 - 110 1.52 12.0 -13.9
404 - 25 - 65 .. 11.1 ..
584 + 1800 + 75 3.45 10.9 16.8
936 + 1300 + 115 2.37 11.1 15.7
1023 + 300 - 10 0.62 10.2 13.8
1700 + 800 + 220 1.16 12.5 12.8
2681 + 700 - 10 1.42 10.7 15.0
2683 + 400 + 65 0.67 9.9 14.3
2841 + 600 - 20 1.24 9.4 16.1
3034 + 290 - 105 0.79 9.0 15.5
3115 + 600 + 105 1.00 9.5 15.5
3368 + 940 + 70 1.74 10.0 16.2
3379 + 810 + 65 1.49 9.4 16.4
3489 + 600 + 50 1.10 11.2 14.0
3521 + 730 + 95 1.27 10.1 15.4
3623 + 800 + 35 1.53 9.9 16.0
4111 + 800 - 95 1.79 10.1 16.1
4526 + 580 - 20 1.20 11.1 14.3
4565 + 1100 - 75 2.35 11.0 15.9
4594 + 1140 + 25 2.23 9.1 17.6
5005 + 900 - 130 2.06 11.1 15.5
5866 + 650 - 215 1.73 11.7 -14.5
------ ---------
Mean 10.5 -15.3
The residuals for the two solutions given above average
150 and 110 km./sec.
and should represent the average peculiar motions of the
individual nebulae and of the groups, respectively. In order to exhibit
the results in a graphical form, the solar motion has been eliminated
from the obsrved velocities and the remainders, the distance terms plus
the residuals, have been plotted against the distances. The run of the
residuals is about as smooth as can be expected, and in general the
form of the solutions appears to be adequate.
The 22 nebulae for which distances are not available can be treated in two ways. First, the mean distance of the group derived from the mean apparent magnitudes can be compared with the mean of the velocities corrected for solar motion. The result, 745 km./sec. for a distance of 1.4 x 10[6] parsecs, falls between the two previous solutions and indicates a value for K of 530 as against the proposed value, 500 km./sec.
Secondly, the scatter of the individual nebulae can be examined by assuming the relation between distances and velocities as previously determined. Distances can then be calculated from the velocities corrected for solar motion, and absolute magnitudes can be derived from the apparent magnitudes. The results are given in table 2 and may be compared with the distribution of absolute magnitudes among the nebulae in table 1, whose distances are derived from other criteria. N. G. C. 404 can be excluded, since the observed velocity is so small that the peculiar motion must be large in comparison with the distance effect. The object is not necessarily an exception, however, since a distance can be assigned for which the peculiar motion and the absolute magnitude are both within the range previously determined. The two mean magnitudes, -15.3 and -15.5, the ranges, 4.9 and 5.0 mag., and the frequency distributions are closely similar for these two entirely independent sets of data; and even the slight difference in mean magnitudes can be attributed to the selected, very bright, nebulae in the Virgo Cluster. This entirely unforced agreement supports the validity of the velocity-distance relation in a very evident matter. Finally, it is worth recording that the frequency distribution of absolute magnitudes in the two tables combined is comparable with those found in the various clusters of nebulae.

The results establish a roughly linear relation between velocities and distances among nebulae for which velocities have been previously published, and the relation appears to dominate the distribution of velocities. In order to investigate the matter on a much larger scale, Mr. Humason at Mount Wilson has initiated a program of determining velocities of the most distant nebulae that can be observed with confidence. These, naturally, are the brightest nebulae in clusters of nebulae. The first definite result,[4] v = + 3779 km./sec. for N. G. C. 7619, is thoroughly consistenct with the present conclusions. Corrected for the solar motion, this velocity is +3910, which, with K = 500, corresponds to a distance of 7.8 x 10[6] parsecs. Since the apparent magnitude is 11.8, the absolute magnitude at such a distance is -17.65, which is of the right order for the brightest nebulae in a cluster. A preliminary distance, derived independently from the cluster of which this nebula appears to be a member, is of the order of 7x10[6] parsecs.
New data to be expected in the near future may modify the significance of the dpresent investigation or, if confirmatory, will lead to a solution having many times the weight. For this reason it is thought premature to discuss in detail the obvious consequences of the present results. For example, if the solar motion with respect to the clusters represents the rotation of the galactic system, this motion could be subtracted from the results for the nebulae and the remainder would represent the motion of the galactic system with respect to the extra-galactic nebulae.
The outstanding feature, however, is the possibility that the velocity-distance relation may represent the de Sitter effect, and hence that numerical data may be introduced into discussions of the general curvature of space. In the de Sitter cosmology, displacements of the spectra arise from two sources, an apparent slowing down of atomic vibrations and a general tendency of material particles to scatter. The latter involves an acceleration and hence introduces the element of time. The relative importance of these two effects should determine the form of the relation between distances and observed velocities; and in this connection it may be emphasized that the linear relation found in the present discussion is a first approximation representing a restricted range in distance.
[2]Harvard Coll. Obs. Circ., 294, 1926.
[3]Mon. Not. R. Astr. Soc., 85, 1925 (865-894).
[4]These PROCEEDINGS, 15, 1929 (167).