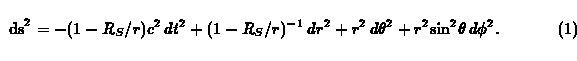
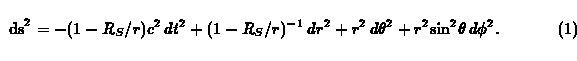
Here ds is a metric measure of coordinate distance r, coordinate time t and coordinate angles theta and phi. The term R_S, the Schwarzschild radius, refers to the radius of a black hole event horizon, and c refers to the local speed of light. R_S is directly proportional to the mass that creates the metric through R_S = 2GM/c^2, where G is the gravitational constant and M is the mass interior to r.
For a photon, ds^2 = 0. Combining this with the conservation of angular momentum allows one to express the deflection angle phi of a photon moving in a gravitational field [16] as
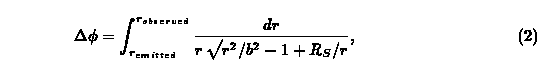
where b is a constant over the trajectory of the photon path, corresponding to a linear projected impact parameter of a photon at infinity for a photon that escapes. This impact parameter can be visualized by assuming that when the photon is far from the gravitating object it travels in a straight line; the impact parameter is the distance between the closest approach of the continuation of this straight line and the center of the gravitating object. Note that Delta phi is not the extra angle deflected by the lens but the total change in the phi angle between the observer and the source, emitted at radial coordinate r_emitted and observed at radial coordinate r_observed. This angle is measured with the lens at the vertex, and includes gravitational deflection. Therefore, for example, a source seen by an observer just over the limb of a lens which has only a small mass, and hence a negligible effect of the trajectory of the photon, has a Delta phi near pi.
An important radius is found from Eq. (2) when Delta phi diverges to infinity. Here a photon will circle the massive star at the photon sphere. The exact location of the photon sphere is R_P = 1.5 R_S. Note that a "normal" neutron star with a relatively weak external gravitational field does not have a photon sphere. Were it somewhat more compact, it would have a photon sphere, and were it even more compact, it would have an event horizon and be called a black hole. For black holes and the "ultracompact" neutron stars considered below, however, these circular photon orbits can exist.
Photons circling at the photon sphere are not in a stable orbit [16] - any small perturbation will cause them to spiral either in or out. Photons emitted from infinity with impact parameters slightly greater than R_B = 3^(1.5) R_S / 2 will spiral around the compact star near the photon sphere and then spiral out. Photons emitted from infinity with impact parameters slightly less than R_B will spiral around near the photon sphere and then spiral in, eventually colliding with the neutron star surface or falling into the black hole. It is also possible for a photon to be emitted from a ultracompact neutron star surface, orbit near the photon sphere, and then spiral back in again impacting the surface. These describe, in general all of the distinct cases of photon orbit near an ultracompact neutron star. All shorter photon trajectories will lie on one of these paths.
Stated differently, the three cases of photon orbits near a gravitating body can be classified as: "always outside the photon sphere," "crossing the photon sphere," and "always inside the photon sphere." The first is the case of a photon passing the neutron star or black hole, reaching a critical radius R_c, and then escaping again toward infinity. In this case the photon does not reach or cross the photon sphere. Its distance from the star decreases monotonically until R_c, and then increases monotonically thereafter. The second case is that of a photon continuing to come toward the neutron star (or black hole) until it impacts the surface (or falls through the event horizon). Here its distance decreases monotonically. The third case is that of a photon emitted from the surface of a strong gravity neutron star, reaching a critical radius R_c, and then falling back down and again impacting the neutron star surface. This critical radius is given by the cubic equation solution [9]
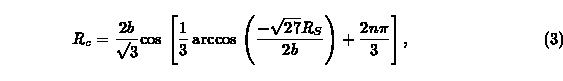
where n = 0 is for the first case and n = 2 is for the third case.
Photons climbing out of a gravitating object become less energetic. This loss of energy is known as a "redshifting", as photons in the visible spectrum would appear more red. Similarly, photons falling into a gravitational field become more energetic and exhibit a blueshifting. The observed energy E_observed at radius r_observed of a photon emitted at radius r_emitted with energy E_emitted is [7]
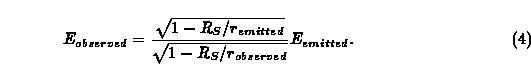
Note that the magnitude of the redshifting (blueshifting) effect is not a function of the emitted angle or the received angle of the photon - it depends only on how far radially the photon had to climb out of (fall into) the potential well. Also note that the power received from a continuously emitting source would have an additional factor of [(1 - R_S/r_emitted) / (1 - R_S/r_observed)]^(1/2) caused by the relative differences in the perceived rate of the number of photons emitted per unit time.
The effect a gravitational field would have on the actual perceived color of an object is more complex, however, as it depends on the distribution of photons emitted from the source at different energies relative to the sensitivity of the observer to measuring photons of different energies. For example, an object that would be described as green might be very bright in the ultra-violet - but this would not normally be perceived, as people cannot see the ultra-violet. Were this object put in a strong gravitational field and viewed from far away, so that the photons would be significantly redshifted, the strong ultra-violet emission could be shifted into violet emission and the object would look more blue, even though its light has been redshifted. This is an exceptional case, however, and redshifted objects may indeed appear more red.