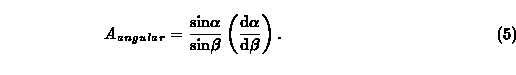
A gravitational field may cause an extended source to appear not only multiply imaged but also greatly distorted. There is at least one feature that each of the images will maintain, however, that is the same as the original source: red- or blueshift corrected surface brightness. Any radiative process preserves the specific intensity along the beam. [17] When gravity is involved, power along the beam is not conserved, it grows or shrinks in accordance with the red- or blueshift. What is conserved is the "corrected surface brightness" B_c = B_r / (1 - R_S/r), where B_r is the measured surface brightness at r.
For example, if an observer originally saw an unlensed circular source with constant surface brightness, a gravitational field could cause the observer to see multiple, elongated, images. Each image would have, however, the same corrected surface brightness (B_c) as the original unlensed source.
The net flux that reaches the observer from any single image of the source can be either more or less than the original unlensed flux of the source. Each image will undergo an amplification A, with A not constrained to be greater than unity. [9] This means that when considered together, the images of a source seen near a large gravitational field can have more or less flux than the same source seen without the intervening gravitational field. Essentially, there are two types of amplifications a source can be seen to undergo: time distortion induced amplifications A_time, related directly to the slowing of time in a gravitational field that causes photons to change both their energy (red- or blueshift) and the perceived arrival rate (and hence the source's perceived power integrated over all wavelengths), and amplifications in the apparent angular size of the source, A_angular. The total amplification will be designated A_total = A_time * A_angular. In the convention used here, all amplifications will be greater than zero.
Time induced amplifications result when the observer is at a different r from the lens center than the source. When considering only time induced amplifications, the total bolometric (incorporating all wavelengths) power received will then be changed by an amount A_time = (1-R_S/r_emitted)/(1-R_S/r_observed).
For the sources near perfect lens - observer alignment, the angular amplification effects typically dominate over time induced amplification effects. Angular amplifications can be computed from the deflection angle Eq. (2). If a large change in angular position on the observer's sky corresponds with a small change in the angular position at the (unlensed) source location, then the source will appear to be angularly elongated and hence amplified. Similarly a source can be angularly deamplified, but this will be referred to as an angular amplification of less than unity. Angular amplification effects should be computed on the spherical sky of the observer, and so would be given by [8]
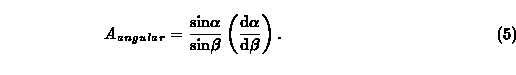
Here beta represents the angular distance between the lens and the source on the observer's sky in the absence of the gravitational field of the lens, while alpha represents this distance in the presence of the gravitational field and light deflection. The change in this angular distance, d alpha/d beta can be found by application of Eq. (2). When bending angles due to gravitational effects are small, this reduces to the amplification formulae given by Refsdal [18] and Liebes. [19]
The net angular amplification of all the images of a single source can also be either more or less than the original unlensed flux of the source. [7, 20] This is because the gravitational field does not change the fact that the observer still observes the same total angular area as before: 4 pi steradians. Therefore if the apparent angular area from some sources is greater than without the gravitational field, then there must be other sources with apparent angular area which is lower, to compensate. In practice, only relatively few images from sources that are near the observer - lens line will have angular amplifications very large (A_angular >> 1), while the rest of the sources in the sky will be slightly deamplified (A_angular < ~ 1).
The total flux received by an observer from all the sky can again be either more or less than the original unlensed flux of all the sky. [20] A gravitational field does not create photons - it just redistributes and (red- or) blueshifts them. The observed angular redistribution and the relative time distortions, however, now act in opposite directions. For the background sky, A_angular < 1, because now its angular area, which used to occupy the observer's entire field of view (4 pi steradians) in the absence of gravity, is now less by the amount of the angular size of the photon sphere of the lens. However, the photons from the sky, because of the blueshifting, are relatively more energetic and arriving relatively more often, so that A_time > 1. [7]
In other words, the background sky takes up less of the observer's sky, but the observer receives more photons per unit area, and each photon is of higher energy. Do these effects exactly cancel? No. It turns out that all observers will measure A_total > 1, with the closer the oberver the greater is A_total.
It is not generally appreciated that there can be an infinite number of Einstein rings. In fact, there can be an infinite number of Einstein rings for each set of collinear observer, lens, and source points. The only Einstein ring currently discussed in the literature is the most prominent one that occurs at precise observer - lens - source alignment, where Delta phi = pi. Here light emitted at a specific angle from the source would be slightly deflected by the gravitational field of the lens to reach the observer. Were the source light emitted at a different angle the lens would either not be able to bend the light enough to reach the observer or too much. Since the exact observer, lens, source alignment is symmetric about the line connecting them, this source would be seen as an annular ring. This ring will be referred to as the first Einstein ring. (Later the term Einstein ring will be even additionally labelled by the relative radius of the source.)
Other Einstein rings can be seen angularly closer to the center of the lens. Photons from the third Einstein ring (the second Einstein ring will be defined two paragraphs below) have fully circled the lens once near the photon sphere before coming to the observer. In fact, the path of these photons crosses itself. It is possible for photons to orbit the lens an arbitrarily large number of times before coming to the observer, and each of these orbits corresponds to an Einstein ring. Therefore there are innumerable Einstein rings for this specific observer - lens - source configuration. Each Einstein ring is seen successively closer to the apparent photon sphere position. The more times the photon must circle the neutron star or black hole before reaching the observer, the more precise the direction of its emission must have been emitted to attain this trajectory, the less likely any photon will take this trajectory, the "dimmer" the Einstein ring. For this reason the higher order Einstein rings will usually carry little light when compared to the lower order Einstein rings. In fact, the relative brightness of each Einstein ring decreases exponentially. [10]
The first Einstein ring can be seen not only in a high gravity environment, but also in a low gravity environment quite a distance from much larger objects, such as normal stars, galaxies, and clusters of galaxies. In fact, complete first Einstein rings have actually been seen for radio galaxies. [22] A good review of extragalactic measurements of gravitational lens effects is given by Blandford and Narayan. [23]
Another set of Einstein rings is observable when the observer and source are on the same side of the lens. Then, for compact sources such as an ultracompact neutron star, light from behind the observer is able to make a "U-turn" around the neutron star and come back to be visible to the observer. The Einstein ring seen from these light trajectories will be called the second Einstein ring, since it is seen between the first and third Einstein rings, and is brighter than the third but dimmer than the first. The fourth Einstein ring in this set is created when light does a "U-turn" near the photon sphere of the lens, then goes all the way around the lens again near the photon sphere, and finally comes to the observer. Note that there is a critical minimum (or maximum for observers inside the photon sphere) distance for the photon just like in the case of slight deflection, that is given by Eq. (3). There are also an infinite number of higher order Einstein rings of this type. As before, however, these Einstein rings carry relatively little power when compared to the lower order Einstein rings.
It is convenient to also define the zeroth Einstein ring, where light from a source located on the line from the lens through the observer comes directly undeflected to the observer along a radial line (Delta phi = 0). This Einstein "ring" is actually a single point on the observer's sky. It differs from the other Einstein rings in that its angular amplification (of a collinear point source) is not formally divergent.
Note that a single source located precisely on the opposite side of the lens from the observer would create only the first, third, fifth, etc. (i.e. odd numbered) Einstein rings. A single source located on the same side of the lens as the observer would create the zeroth, second, fourth, etc. (i.e. even numbered) Einstein rings.
In general, the position of each set of Einstein rings will be different for each specific source radius from the lens, relative to the observer position. For example, a point source at infinity directly behind the lens from the observer would create a complete set of odd numbered Einstein rings. A point source located a small, finite distance from the lens (but still directly behind the lens) would create a different set of odd numbered Einstein rings. Each set of Einstein rings can thus be labeled by the location of the source sphere. Sources at infinity will be referred to "sky" Einstein rings. For sources on the surface of the lens, the term "surface" Einstein rings will be used. In general, the convention will be taken of labelling each Einstein ring by the name or radius of the source sphere.
Mathematically, an Einstein ring will always occur when the total deflection angle due to gravitation Delta phi (Eq. 2) is equal to any integer multiple of pi radians. [7] Note that the Einstein rings are theoretical constructs and would only be visible were a source placed precisely on the observer-lens line, which for any small source is unlikely.
If the angular radius of an opaque lens is larger than the angular radius of the first Einstein ring for the source, then this ring will exist. If the radius of the lens is smaller than the radius of the first Einstein ring but larger than the other Einstein rings, then only the first Einstein ring will exist. If the radius of the lens is small enough so that the lens exhibits a photon sphere, however, an infinite number of Einstein rings exist. This is because a subsequent Einstein ring exists for each revolution of the lens a photon orbit can take, and theoretically, since all of these orbits are contained completely above the photon sphere, it can take an infinite number of them.
It should be noted that the existence of an Einstein ring may depend on the relative positions of the lens, observer, and source, while the existence of the photon sphere or event horizon does not depend on these relative positions. It is possible for the first sky Einstein ring to exist for a given observer looking toward a neutron star lens, but as the observer moves closer to the neutron star the angular size of the surface becomes larger than the angular size of this Einstein ring. For black holes and neutron star's compact enough to have a photon sphere, though, the photon sphere is a real entity - photons do circle there - whether or not an observer is there to see them.
If the radius of the lens is small enough so that the lens exhibits a photon sphere, an infinite number of images can be seen of the source, no matter its location. One image of the source comes to the observer relatively undeflected. This image is between the zeroth and first Einstein rings and will be referred to as the primary image. A second image comes around the opposite limb of the lens from the first image, and therefore will appear to the observer 180 degrees around the face of the lens from the first image. This secondary image will always be located between the first and second Einstein rings. A third image comes around the same limb as the first image and is seen even closer to the apparent position of the photon sphere. This image has circled the neutron star or black hole fully once before reaching the observer, and its location is always between the second and third Einstein rings. The photon path for this image (and all higher order images) crosses itself. A fourth image occurs closer to but outside of the same limb as the second image, but has fully circled the lens once in the opposite direction. There is a subsequent image for each revolution of the lens a photon orbits takes, and theoretically it can take an infinite number of them. In practice, these multi-revolution images have little power and would be vanishingly hard to see. [9]
Each set of images contained between successive Einstein rings is converted into "mirror writing" with respect to the images between the previous two Einstein rings. For example, if the source was a book, then the book would be visible with relatively minor distortions in its primary image - between the zeroth and first book Einstein rings. For the secondary image, between the first and second book Einstein rings, the book would appear in mirror writing, but right side up. The mapping of the entire sphere onto the annular ring between the two book Einstein rings would also cause prominent distortions. The third image of the book, between the second and third book Einstein rings, would appear in normal writing again (neither in mirror writing nor inverted), but even more distorted because of the decreased relative angular area between these two book Einstein rings. A discussion of the parity of lensed images for the brightest two images of the point lens (considered here) as well as other gravitational lens types, can be found in Blandford and Kochanek. [24]
Therefore, for a compact enough neutron star, one can see the whole neutron star surface. [5] An observer can see the complete surface of a lens (exactly once) when the first surface Einstein ring is the same angular size as the surface of the lens. (A derivation of the angular size of a sphere of mass M, radius R_* at distance D is given in the Appendix.) When the second surface Einstein ring has equal angular size to the apparent angular size of the lens surface, two complete images of the lens surface are visible.
Any lens which has a first surface Einstein ring is completely incapable of blocking light from any source. These objects cannot "eclipse" anything. This is why a neutron star in a well separated binary system can never block the light of its binary companion.
Less stringently, any lens with a first sky Einstein ring is incapable of blocking light from the background sky. Almost all stars in our galaxy are thus incapable of blocking light from random superpositions of background objects. For example, no supernovae in other galaxies are missed because they are "eclipsed" by a random superposition of a foreground star in the Milky Way Galaxy. Were such a chance superposition to occur (it is very unlikely), the supernova would be greatly amplified by the gravitational field of the intervening star rather than diminished by an "eclipse" effect. With respect to distant sources, these stars are easily compact enough to show a first Einstein ring to a distant observer, and are therefore incapable of blocking the source's light.
Every star in existence, besides the Sun but including even the nearest stars, has a first sky Einstein ring with respect to an earth bound observer. The small angular size of this Einstein ring is below optical resolution, but not below the angular resolution of many radio observations. The gravity of these normal stars is strong enough to bend the background light around them and cause distant sources to be visible to the observer. Almost none of the nearby stars, however, would show a second sky Einstein ring, unless they were a neutron star or black hole. Were the star compact enough to have a photon sphere surrounding it, then, theoretically, an infinite number of sky Einstein rings (and hence sky images) would be visible.
Amusingly, there is only a single case where observers can see only a single image of themselves - and this is the case that is well known [25] - when observers are at the photon sphere! Here all the self Einstein rings actually merge with the photon sphere to form a single observer image.
Observers who see themselves would be viewing themselves with high amplification. This is because the self images observers would see would be on or near Einstein rings - which carry the highest amplifications. Therefore gravity has become a powerful microscope! When at the photon sphere observers can microscopically view the backs of their heads, and when far away observers can microscopically view their own eyes. This is because the light that returns to the observer has left on a nearly radial trajectory - and the part of the observer most nearly radial is the observer's own eye. When close to and inside the photon sphere, observers can inspect annular rings on their heads (or spacecrafts).
The second case that will be described is that of visiting a black hole. This case is more complex in that many bound and unbound photon orbits exist near the black hole. There is, however, a somewhat simpler aspect to describing this case than the previous one in that one does not have to track surface feature distortions for a black hole.
The third and last case that will be described is that of visiting a ultracompact neutron star - one with an extreme equation for its interior structure that allows a mean density so high the star has a photon sphere. This is the most complicated case of all to describe as it involves all three types of photon orbits described above as well as requiring a description of both the sky and surface feature distortions.
To more clearly delineate what the viewer would see, a set of computer generated figures were created that document the distortion effects in terms of familiar icons. In these illustrations, the sky in the background behind the high gravity star was taken to be the night sky as viewed from present-day earth. More specifically, the background sky is taken from the Bright Star Catalogue, [26] allowing all stellar images as dim as 5th magnitude to be seen, and stellar images as dim as 7th magnitude may be amplified into visibility. In the two cases of neutron stars, a map of the earth was projected onto the surfaces of the stars and allowed to distort. These figures are, in many aspects, fully general relativistically correct. The resolution of the figures is about 3 arcminutes (0.05 degrees).
Stellar image brightnesses are shown by the area the stellar image takes on the plots: the area is directly proportional to the flux the observer would receive from the image. It was impossible to change the pixel brightness, so many of the single pixel images would actually be seen dimmer than shown in the figures. Stellar images were allowed to get brighter or dimmer by angular amplification effects, but time induced amplification effects have been suppressed.
Note that for A_angular > 1 the stellar image flux would actually be seen as an increase in angular area of the image, so that the amplified angular area of the stellar images in the computer generated plots are, in this sense, realistic. However, the distortions in the amplified images would not be readily observable, as these background images would be unresolved by the viewer and hence indistinguishable from point sources. A small amplification would not cause the image to be resolved. Stellar images will therefore always be depicted as circles, even when they undergo angular amplification, as these convey best the idea of an unresolved point sources.
Only the two brightest images of all sources were tracked by the computer programs used. All stars originally 5th magnitude or brighter are plotted as secondary images, no matter their magnitude after gravitational distortion. Stars originally 5th magnitude are only plotted as primary images, however, if their final post-lensed magnitude was 5 or brighter. Higher order images undergoing larger angular amplification could potentially be visible but one would need significantly better angular resolution so see them (the only exception to this will be Fig. 2p), so they will be suppressed. An angular amplification limit of a factor of 100 was placed on all images for plotting purposes.
The hypothetical "camera" used in the simulations is somewhat fanciful but has several defining characteristics. First of all the camera is asymptotically small so that no general relativistic light bending effects are important over the length of the camera. The camera's field of view is 90 degrees across the middle of the picture. Lastly, the illustrations that follow, produced by the "camera," have been "flat-fielded" so that angular area on the spherical sky is directly proportional to spatial area on the flat page.